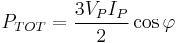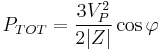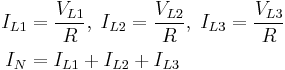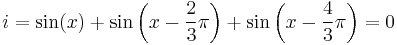Three-phase
In electrical engineering, three-phase electric power systems have at least three conductors carrying voltage waveforms that are 2π⁄3 radians (120°, 1⁄3 of a cycle) offset in time. In this article angles will be measured in radians except where otherwise stated.
Contents |
Definitions
Let  be the instantaneous phase of a signal of frequency
be the instantaneous phase of a signal of frequency  at time
at time  :
:
Using this, the waveforms for the three phases are
where 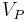 is the peak voltage and the voltages on L1, L2 and L3 are measured relative to the neutral.
is the peak voltage and the voltages on L1, L2 and L3 are measured relative to the neutral.
Balanced loads
Generally, in electric power systems, the loads are distributed as evenly as is practical between the phases. It is usual practice to discuss a balanced system first and then describe the effects of unbalanced systems as deviations from the elementary case.
Star connected systems with neutral
This refers to a system with a resistive load  between each phase and neutral.
between each phase and neutral.
Constant power transfer
An important property of three-phase power is that the power available to a resistive load, 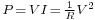 , is constant at all times.
, is constant at all times.
To simplify the mathematics, we define a nondimensionalized power for intermediate calculations, 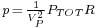
Hence (substituting back):
since we have eliminated  we can see that the total power does not vary with time. This is essential for keeping large generators and motors running smoothly. Actually, the load need not be resistive for achieving a constant instantaneous power since, as long as it is balanced or the same for all phases, it may be written as
we can see that the total power does not vary with time. This is essential for keeping large generators and motors running smoothly. Actually, the load need not be resistive for achieving a constant instantaneous power since, as long as it is balanced or the same for all phases, it may be written as
so that the peak current is
for all phases and the instantaneous currents are
Now the instantaneous powers in the phases are
Using angle subtraction formulae:
which add up for a total instantaneous power
Since the three terms enclosed in square brackets are a three-phase system, they add up to zero and the total power becomes
or
No neutral current
For the case of equal loads on each of three phases, no net current flows in the neutral. The neutral current is the sum of the phase current.
We define a non-dimensionalized current, 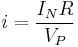 :
:
Hence also 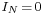
Since we have shown that the neutral current is zero we can see that removing the neutral core will have no effect on the circuit, provided the system is balanced. Such connections are generally used only when the load on the three phases is part of the same piece of equipment (for example a three-phase motor), as otherwise switching loads and slight imbalances would cause large voltage fluctuations.
Unbalanced systems
Practical systems rarely have perfectly balanced loads, currents, voltages or impedances in all three phases. The analysis of unbalanced cases is greatly simplified by the use of the techniques of symmetrical components. An unbalanced system is analyzed as the superposition of three balanced systems, each with the positive, negative or zero sequence of balanced voltages.
Harmonics
Prior to the invention of fluorescent lighting, it was common practice to provide a neutral conductor for three-phase systems rated at half the current carrying capacity of the phase conductors. With linear loads, the neutral only carries the current due to imbalance between the phases, which by design is not large. Fluorescent lighting and other non linear device draw current with a substantial third harmonic component. This third harmonic (and all harmonics divisible by three) current are in-phase on all the supply phases. These triplen currents sum in the neutral to three times the individual phase (third harmonic) currents. The neutral conductor must then have the same current rating as the phase conductors.
Switched mode power supplies
A number of switch mode power supplies draw current in pulses near the peak of the supply voltage. This narrow current pulse is not wide enough for any sort of cancellation with similar devices on other phases, resulting in neutral currents that can exceed the current of an individual phase. Switch mode power supplies operated on a three-phase system can produce neutral currents of 1.4 times the phase current, even when perfectly balanced in terms of load. These currents are caused by the harmonic currents. In Europe, switched mode supplies are required to have power factor correction to reduce this effect. An additional stage is added to the power supply so that current is drawn over a larger part of the voltage cycle. This is not yet a mandatory requirement in the United States, but the voluntary Energy Star program requires certain compliant power supplies to have a true power factor of at least 0.9.[1]
Revolving magnetic field
Any polyphase system, by virtue of the time displacement of the currents in the phases, makes it possible to easily generate a magnetic field that revolves at the line frequency. Such a revolving magnetic field makes polyphase induction motors possible. Indeed, where induction motors must run on single-phase power (such as is usually distributed in homes), the motor must contain some mechanism to produce a revolving field, otherwise the motor cannot generate any stand-still torque and will not start. The field produced by a single-phase winding can provide energy to a motor already rotating, but without auxiliary mechanisms the motor will not accelerate from a stop when energized.
A rotating magnetic field of steady amplitude requires that all three phase currents are equal in magnitude and accurately displaced one-third of a cycle in phase. Unbalanced operation results in undesirable effects on motors and generators.
Conversion to other phase systems
Provided two voltage waveforms have at least some relative displacement on the time axis, other than a multiple of a half-cycle, any other polyphase set of voltages can be obtained by an array of passive transformers. Such arrays will evenly balance the polyphase load between the phases of the source system. For example, balanced two-phase power can be obtained from a three-phase network by using two specially constructed transformers, with taps at 50% and 86.6% of the primary voltage. This Scott T connection produces a true two-phase system with 90° time difference between the phases. Another example is the generation of higher-phase-order systems for large rectifier systems, to produce a smoother DC output and to reduce the harmonic currents in the supply.
When three-phase is needed but only single-phase is readily available from the electricity supplier a phase converter can be used to generate three-phase power from the single phase supply.
References
- ^ Carol Baroudi et al, Green IT For Dummies, For Dummies, 2009, ISBN 0470386886 page 225
- Stevenson, William D., Jr. (1975). Elements of Power Systems Analysis. McGraw-Hill electrical and electronic engineering series (3rd ed. ed.). New York: McGraw Hill. ISBN 0-07-061285-4.
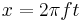
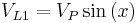
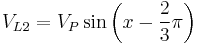
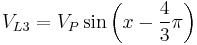
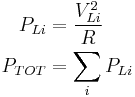
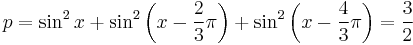
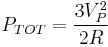
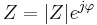
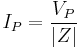
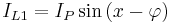
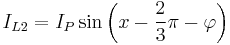
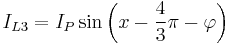
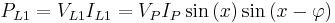
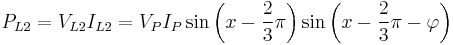
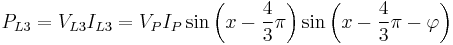
![P_{L1}=\frac{V_P I_P}{2}\left[\cos\varphi-\cos\left(2x-\varphi\right)\right]](/2012-wikipedia_en_all_nopic_01_2012/I/d9f15cb7bc257abd709ed85f4ad52424.png)
![P_{L2}=\frac{V_P I_P}{2}\left[\cos\varphi-\cos\left(2x-\frac{4}{3}\pi-\varphi\right)\right]](/2012-wikipedia_en_all_nopic_01_2012/I/d07c3cbfaf7e7fda545ed98d790ea9a8.png)
![P_{L3}=\frac{V_P I_P}{2}\left[\cos\varphi-\cos\left(2x-\frac{8}{3}\pi-\varphi\right)\right]](/2012-wikipedia_en_all_nopic_01_2012/I/22638ff395b51d78724392c83e3611fe.png)
![P_{TOT}=\frac{V_P I_P}{2}\left\{3\cos\varphi-\left[\cos\left(2x-\varphi\right)%2B\cos\left(2x-\frac{4}{3}\pi-\varphi\right)%2B\cos\left(2x-\frac{8}{3}\pi-\varphi\right)\right]\right\}](/2012-wikipedia_en_all_nopic_01_2012/I/d90aba5b633e00134e20c8364210aacb.png)